Croissance des microtubules

Dernière mise à jour le 2020-07-16 Etude de cas
Données

Contexte biologique

Cette étude se déroule dans le cadre d’une thèse ayant lieu au Francis Crick Institute, London, UK, à propos de protéines qui participent au développement des microtubules en recouvrant leurs extrémités. Ces derniers sont des éléments de cytosquelette impliqués dans l’architecture de la cellule en général et forment le fuseau mitotique lors de la mitose (ou division cellulaire des eucaryotes) en particulier.

L’objectif de l’analyse statistique présentée est de comprendre l’impact d’une de ces protéines sur la croissance des microtubules. La croissance peut s’effectuer sur l’extrémité (end) plus ou moins du microtubule. Nous allons voir que cette croissance se fait préférentiellement sur l’extrémité plus.

Chargement des packages

library(tidyverse) # méta-package contenant beaucoup de fonctions utiles pour la manipulation et la visualisation des jeux de données
library(broom) # nettoie les modèles
library(ggpubr) # ggarrange()
library(multcomp) # comparaisons mutiples

Importation des données

Le fichier importé correspond aux données brutes.

jeu <- read_csv("growth.csv")
## Rows: 437 Columns: 8
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (1): end
## dbl (7): ctrl_buffer, ctrl_NO1, full_length5, C_term5, N_term5, full_length2...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
jeu
## # A tibble: 437 × 8
##    ctrl_buffer ctrl_NO1 full_length5 C_term5 N_term5 full_length2 C_term2 end  
##          <dbl>    <dbl>        <dbl>   <dbl>   <dbl>        <dbl>   <dbl> <chr>
##  1        16.4     20.7         30.1    18.8    17.3         20.2    18.4 Plus 
##  2        20.6     17.2         19.9    19.8    22.8         21.8    18.3 Plus 
##  3        18.3     21.9         23.6    12.6    27.9         18.8    23.9 Plus 
##  4        22.3     28.7         20.8    20.6    23.2         23.7    17.7 Plus 
##  5        20.5     22.7         21.1    18.8    18.8         16.9    15.6 Plus 
##  6        23.6     15.2         23.1    17.4    15.5         18.4    19.4 Plus 
##  7        19.2     19.0         21.0    17.0    23.6         20.8    21.2 Plus 
##  8        16.7     16.6         19.4    22.7    20.3         16.8    18.3 Plus 
##  9        20.3     18.6         14.3    21.4    23.6         18.3    22.9 Plus 
## 10        21.5     18.1         17.9    17.4    23.1         18.3    23.6 Plus 
## # ℹ 427 more rows

D’un point de vue de statisticienne, il y a en fait 3 variables :

  • growth_speed, la vitesse de croissance : ce qui est mesuré
  • treatment, le traitement : Control, NO, FL5, FL2, N5, C5 et C2.
  • end, l’extrémité du microtubule : Plus ou Minus.

Le jeu de données est transformé pour qu’il ait 3 colonnes et une ligne par mesure/observation :

jeu.long <- pivot_longer(jeu, 
 cols = ctrl_buffer:C_term2, # les colonnes à mettre en une seule
 names_to = "treatment", # la colonne où vont les noms des colonnes du jeu d'avant
 values_to = "growth_speed", # la colonne où vont les mesures
 values_drop_na = T # adieu les cases non remplies
 ) %>% 
  mutate(treatment = fct_inorder(treatment)) # modalités de treatment rangée dans l'ordre d'apparition

jeu.long
## # A tibble: 1,917 × 3
##    end   treatment    growth_speed
##    <chr> <fct>               <dbl>
##  1 Plus  ctrl_buffer          16.4
##  2 Plus  ctrl_NO1             20.7
##  3 Plus  full_length5         30.1
##  4 Plus  C_term5              18.8
##  5 Plus  N_term5              17.3
##  6 Plus  full_length2         20.2
##  7 Plus  C_term2              18.4
##  8 Plus  ctrl_buffer          20.6
##  9 Plus  ctrl_NO1             17.2
## 10 Plus  full_length5         19.9
## # ℹ 1,907 more rows

Visualisation

Les données brutes sont regardées en premier, car des intervalles de confiance ou des boxplot peuvent cacher des choses.

ggplot(jeu.long) +
  aes(x = treatment, y = growth_speed) + # rôle des variables
  geom_jitter(width = 0.3, height = 0, alpha = 0.7) + # une observation = un point, avec un bruit horizontal et un peu de transparence (pour les superpositions)
  geom_point(stat = "summary" 
                  , fun = "mean"
                  , colour = "red"
                  , size = 2
                  ) + # la moyenne est en rouge
  facet_wrap(~ end) + # un graphique par End
  labs(y = "Growth speed (nm/s)", x = "") + # noms des axes
  theme(axis.text.x = element_text(angle = 45, hjust = 1, vjust = 1)) # orientation des labels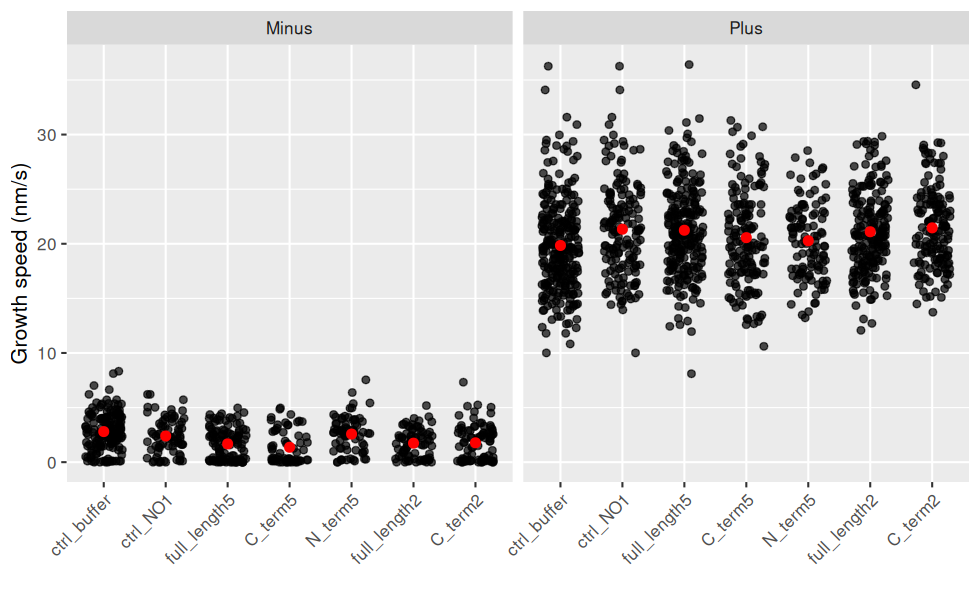

Et avec les intervalle de confiance (bootstrap : aucune hypothèse sur les données sous-jacentes) et les échelles différentes pour les Ends :

ggplot(jeu.long) +
  aes(x = treatment, y = growth_speed) + # rôle des variables
  geom_pointrange(stat = "summary" 
                  , fun.data = "mean_cl_boot" # bootstrap
                  ) + # le point correspond à la moyenne
  facet_wrap(~ end, scales = "free_y") + # un graphique par End
  labs(y = "Growth speed (nm/s)", x = "") + # noms des axes
  theme(axis.text.x = element_text(angle = 45, hjust = 1, vjust = 1)) # orientation des labels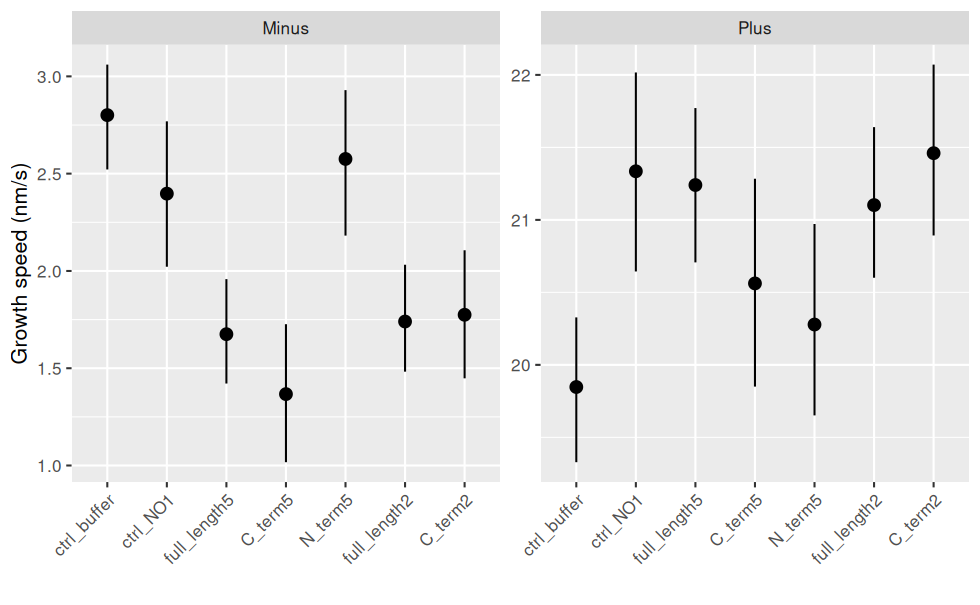

Modélisation

Modèle complet

On suppose une distribution linéaire de la vitesse. On suppose également l’indépendance des mesures. On voit que ce n’est pas exact d’ores et déjà, puisque les vitesses faibles (minus) sont minorée par 0.

mod.complet <- lm(growth_speed ~ treatment * end, data = jeu.long)
glance(mod.complet)
## # A tibble: 1 × 12
##   r.squared adj.r.squared sigma statistic p.value    df logLik    AIC    BIC
##       <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl>  <dbl>  <dbl>
## 1     0.872         0.871  3.41      998.       0    13 -5064. 10158. 10242.
## # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
tidy(mod.complet)
## # A tibble: 14 × 5
##    term                          estimate std.error statistic  p.value
##    <chr>                            <dbl>     <dbl>     <dbl>    <dbl>
##  1 (Intercept)                      2.80      0.264    10.6   1.26e-25
##  2 treatmentctrl_NO1               -0.404     0.476    -0.848 3.97e- 1
##  3 treatmentfull_length5           -1.13      0.416    -2.70  6.90e- 3
##  4 treatmentC_term5                -1.43      0.496    -2.89  3.86e- 3
##  5 treatmentN_term5                -0.225     0.488    -0.462 6.44e- 1
##  6 treatmentfull_length2           -1.06      0.470    -2.26  2.40e- 2
##  7 treatmentC_term2                -1.03      0.447    -2.29  2.19e- 2
##  8 endPlus                         17.0       0.336    50.8   0       
##  9 treatmentctrl_NO1:endPlus        1.89      0.586     3.23  1.26e- 3
## 10 treatmentfull_length5:endPlus    2.52      0.517     4.88  1.17e- 6
## 11 treatmentC_term5:endPlus         2.15      0.605     3.55  3.94e- 4
## 12 treatmentN_term5:endPlus         0.656     0.623     1.05  2.92e- 1
## 13 treatmentfull_length2:endPlus    2.32      0.568     4.07  4.82e- 5
## 14 treatmentC_term2:endPlus         2.64      0.566     4.66  3.31e- 6

Vérification des hypothèses de normalité sur les résidus :

# Création d'une fonction traçant les ggplots de vérification d'un lm (à la manière de plot.lm())
verifier_lm <- function(modele) {
  # résidus standardisés en fonctions des valeurs prédites
  hyp1 <- ggplot(modele, aes(.fitted, .stdresid)) +
    geom_point() +
    geom_hline(yintercept = 0) +
    geom_smooth(se = FALSE)
  
  # variance des résidus en fonction des valeurs prédites
  hyp2 <- ggplot(modele, aes(.fitted, sqrt(abs(.stdresid)))) +
    geom_point() +
    geom_smooth(se = FALSE)
  
  # qqplot
  hyp3 <- ggplot(modele) +
    stat_qq(aes(sample = .stdresid)) +
    geom_abline()
  
  # residuals vs. leverage avec les distances de cook
  hyp4 <- ggplot(modele, aes(.hat, .stdresid)) +
    geom_point(aes(size = .cooksd)) +
    geom_smooth(se = FALSE, size = 0.5)
  
  ggarrange(hyp1, hyp2, hyp3, hyp4)
}

verifier_lm(mod.complet)

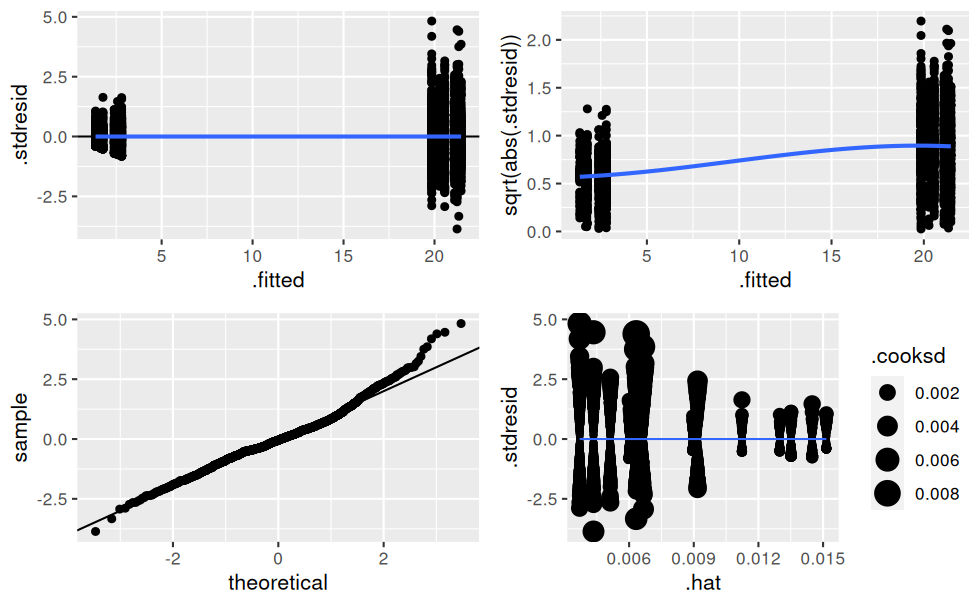
Il y a clairement de l’hétéroscédasticité dans les résidus, c’est-à-dire que leur variance n’est pas constante !

Tranformation de la variable à expliquer Y

Transformation racine carrée de la variable growth_speed, classique en cas d’hétéroscédasticité :

jeu.long <- jeu.long %>% 
  mutate(tgrowth = sqrt(growth_speed))

mod.t <- lm(tgrowth ~ treatment * end, data = jeu.long)
glance(mod.t)
## # A tibble: 1 × 12
##   r.squared adj.r.squared sigma statistic p.value    df logLik   AIC   BIC
##       <dbl>         <dbl> <dbl>     <dbl>   <dbl> <dbl>  <dbl> <dbl> <dbl>
## 1     0.898         0.898 0.522     1293.       0    13 -1467. 2965. 3048.
## # ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
tidy(mod.t)
## # A tibble: 14 × 5
##    term                          estimate std.error statistic   p.value
##    <chr>                            <dbl>     <dbl>     <dbl>     <dbl>
##  1 (Intercept)                     1.55      0.0404    38.5   5.94e-240
##  2 treatmentctrl_NO1              -0.145     0.0729    -1.99  4.69e-  2
##  3 treatmentfull_length5          -0.453     0.0638    -7.10  1.76e- 12
##  4 treatmentC_term5               -0.610     0.0759    -8.04  1.58e- 15
##  5 treatmentN_term5               -0.0678    0.0747    -0.907 3.65e-  1
##  6 treatmentfull_length2          -0.374     0.0719    -5.20  2.20e-  7
##  7 treatmentC_term2               -0.417     0.0685    -6.09  1.36e-  9
##  8 endPlus                         2.88      0.0514    56.0   0        
##  9 treatmentctrl_NO1:endPlus       0.310     0.0897     3.45  5.69e-  4
## 10 treatmentfull_length5:endPlus   0.609     0.0791     7.70  2.14e- 14
## 11 treatmentC_term5:endPlus        0.688     0.0927     7.43  1.68e- 13
## 12 treatmentN_term5:endPlus        0.124     0.0954     1.30  1.93e-  1
## 13 treatmentfull_length2:endPlus   0.520     0.0871     5.97  2.77e-  9
## 14 treatmentC_term2:endPlus        0.602     0.0867     6.95  4.96e- 12
verifier_lm(mod.t)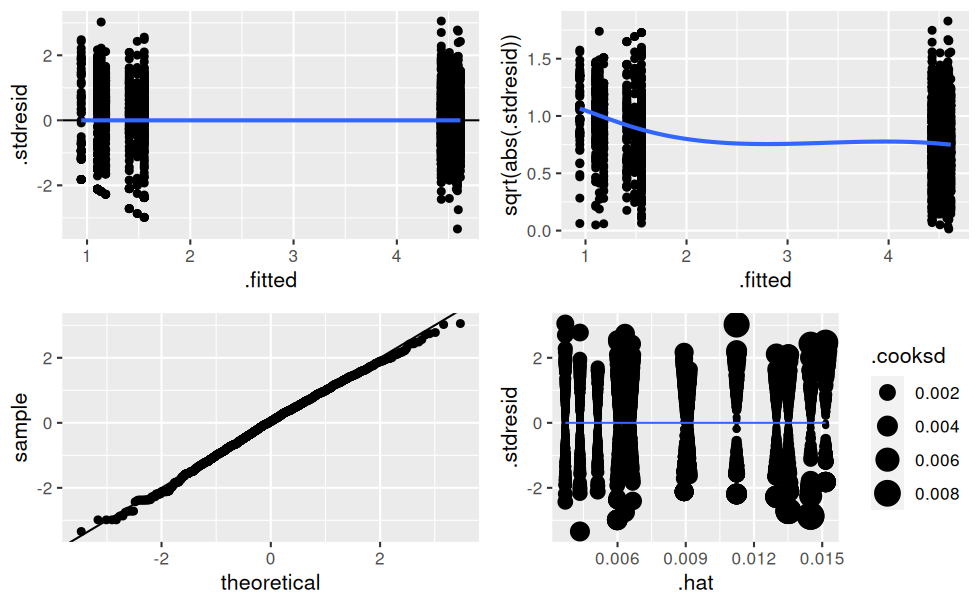

L’AIC et les graphes de vérification des hypothèses sont bien meilleurs maintenant.

Résultats du modèle

On teste les variables explicatives :

anova(mod.t)
## Analysis of Variance Table
## 
## Response: tgrowth
##                 Df Sum Sq Mean Sq   F value    Pr(>F)    
## treatment        6   23.5     3.9    14.341 4.728e-16 ***
## end              1 4527.7  4527.7 16608.383 < 2.2e-16 ***
## treatment:end    6   30.1     5.0    18.390 < 2.2e-16 ***
## Residuals     1903  518.8     0.3                        
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Les 2 variables treatment et end expliquent growth_speed. Il y a également interaction : les traitements n’ont pas le même effet que ce soit sur les extrémités plus ou moins.

Comparaison des traitements

Pour faire les comparaisons multiples deux à deux, il ne faut pas d’interaction dans le modèle. Une nouvelle variable qui combine treatment et end est créée.

jeu.long <- jeu.long %>% mutate(treatend = factor(paste(treatment, end, sep = "/")))
jeu.long
## # A tibble: 1,917 × 5
##    end   treatment    growth_speed tgrowth treatend         
##    <chr> <fct>               <dbl>   <dbl> <fct>            
##  1 Plus  ctrl_buffer          16.4    4.05 ctrl_buffer/Plus 
##  2 Plus  ctrl_NO1             20.7    4.55 ctrl_NO1/Plus    
##  3 Plus  full_length5         30.1    5.48 full_length5/Plus
##  4 Plus  C_term5              18.8    4.34 C_term5/Plus     
##  5 Plus  N_term5              17.3    4.16 N_term5/Plus     
##  6 Plus  full_length2         20.2    4.49 full_length2/Plus
##  7 Plus  C_term2              18.4    4.28 C_term2/Plus     
##  8 Plus  ctrl_buffer          20.6    4.53 ctrl_buffer/Plus 
##  9 Plus  ctrl_NO1             17.2    4.15 ctrl_NO1/Plus    
## 10 Plus  full_length5         19.9    4.46 full_length5/Plus
## # ℹ 1,907 more rows

Modèle équivalent (sans interaction) :

mod.ssinter <- lm(tgrowth ~ treatend, data = jeu.long)
anova(mod.ssinter)
## Analysis of Variance Table
## 
## Response: tgrowth
##             Df Sum Sq Mean Sq F value    Pr(>F)    
## treatend    13 4581.2  352.40  1292.7 < 2.2e-16 ***
## Residuals 1903  518.8    0.27                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Comparaisons multiples 2 à 2 (méthode de Tukey)1 avec une correction de Benjamini-Hocheberg2 pour un risque global alpha de 5% :

comp_treatend <- summary(glht(mod.ssinter, linfct = mcp(treatend = "Tukey")), 
  test = adjusted("BH")
  )

groupes_treatend <- tidy(cld(comp_treatend, level = 0.5)) %>% 
  separate(1, into = c("treatment", "end"), sep = "/")
groupes_treatend
## # A tibble: 14 × 3
##    treatment    end   letters
##    <chr>        <chr> <chr>  
##  1 C_term2      Minus ab     
##  2 C_term2      Plus  c      
##  3 C_term5      Minus d      
##  4 C_term5      Plus  e      
##  5 N_term5      Minus f      
##  6 N_term5      Plus  e      
##  7 ctrl_NO1     Minus g      
##  8 ctrl_NO1     Plus  c      
##  9 ctrl_buffer  Minus h      
## 10 ctrl_buffer  Plus  i      
## 11 full_length2 Minus a      
## 12 full_length2 Plus  c      
## 13 full_length5 Minus b      
## 14 full_length5 Plus  c

Ajout des groupes sur le graphique :

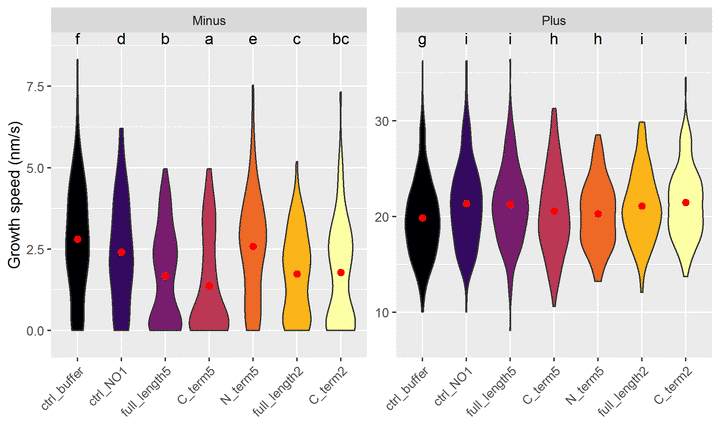
ggplot(jeu.long) +
  aes(x = treatment, y = growth_speed, fill = treatment) +
  geom_violin() +
  geom_point(stat = "summary" 
                  , fun = "mean"
                  , colour = "red"
                  , size = 2
                  ) + # la moyenne est en rouge
  geom_text(data = groupes_treatend, mapping = aes(label = .data$letters, x = treatment), y = Inf, vjust = "top") + # ajout des lettres
  facet_wrap(~ end, scales = "free_y") + # un graphique par end
  labs(y = "Growth speed (nm/s)", x = "") + # noms des axes
  theme(axis.text.x = element_text(angle = 45, hjust = 1, vjust = 1), legend.position = "none") + # orientation des labels
  scale_y_continuous(expand = expansion(mult = 0.1)) + # élargir l'échelle pour laisser de la place aux lettres
  scale_fill_viridis_d(option = "B") # échelle de couleurs distingables par les personnes atteintes de daltonisme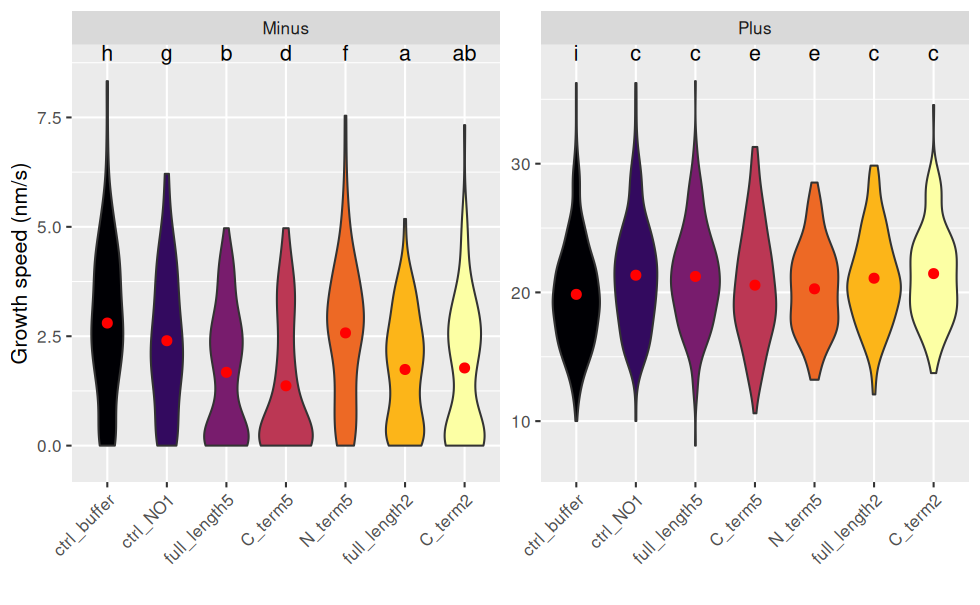

Pour interpréter les lettres : deux combinaisons de traitement/end ayant une lettre en commun ne sont pas statistiquement différentes. Inversement, s’il n’y a aucune lettre en commun, on peut dire que qu’elles sont statistiquement différentes au risque de 5%.

Exemples :

  • Les vitesses de minus sont toutes statistiquement différentes de plus.
  • Pour minus : C2 n’est pas différent de FL5 et FL2, sinon tous les autres traitement sont différents 2 à 2.
  • Pour plus : Tout le monde est différent du ctrl_buffer ; C5 et N5 ne sont pas différents .

NB : les intervalles de confiance se recoupent, mais ne prennent pas en compte la transformation racine carrée de growth_speed, d’où le choix de représenter un violin plot.

Références

1.
Hothorn, T., Bretz, F. & Westfall, P. Simultaneous inference in general parametric models. Biometrical Journal 50, 346–363 (2008).
2.
Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal statistical society: series B (Methodological) 57, 289–300 (1995).
3.
Wickham, H. et al. Welcome to the tidyverse. Journal of Open Source Software (2019).
Comprendre
Anna Doizy
Anna Doizy
Chercheuse, consultante et formatrice freelance
Libre comme l’R

Méthodologie scientifique et analyses de données statistiques