Les comparaisons de moyennes avec emmeans
1 Rappel sur les données
Reprenons le plan factoriel complet de l’introduction à l’ANOVA.
Nous voulions comprendre la variabilité du rendement de la canne à sucre sur 3 années consécutives et pour 3 traitements différents. Il y a 3 répétitions (3 parcelles) pour chaque combinaison année/traitement.
# chargement des packages
library(tidyverse)
library(emmeans)
library(skimr)
# création d'un jeu de données bidon
set.seed(123) # pour fixer l'aléatoire et retrouver le même jeu de données
jeu <- tibble(
Traitement = rep(LETTERS[1:3], each = 9) %>% factor(),
Annee = paste0("N", rep(1:3, times = 3, each = 3)) %>% factor(),
Rendement = c(rnorm(9, mean = 30, sd = 10), rnorm(9, mean = 5, sd = 10), rnorm(9, mean = 10, sd = 10))
)
skim(jeu) # équivalent plus évolué de summary() ;-)| Name | jeu |
| Number of rows | 27 |
| Number of columns | 3 |
| _______________________ | |
| Column type frequency: | |
| factor | 2 |
| numeric | 1 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| Traitement | 0 | 1 | FALSE | 3 | A: 9, B: 9, C: 9 |
| Annee | 0 | 1 | FALSE | 3 | N1: 9, N2: 9, N3: 9 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| Rendement | 0 | 1 | 14.38 | 15.38 | -14.67 | 3.23 | 9.98 | 23.76 | 47.15 | ▁▇▂▅▁ |
Pour rappel, voici un graphique pour représenter les données :
# visualisation des données
ggplot(jeu) +
aes(x = Traitement, y = Rendement) +
geom_boxplot(fill = "transparent", width = 0.4, outlier.shape = NA) +
geom_point(aes(color = Annee), position = position_dodge(width = 0.3))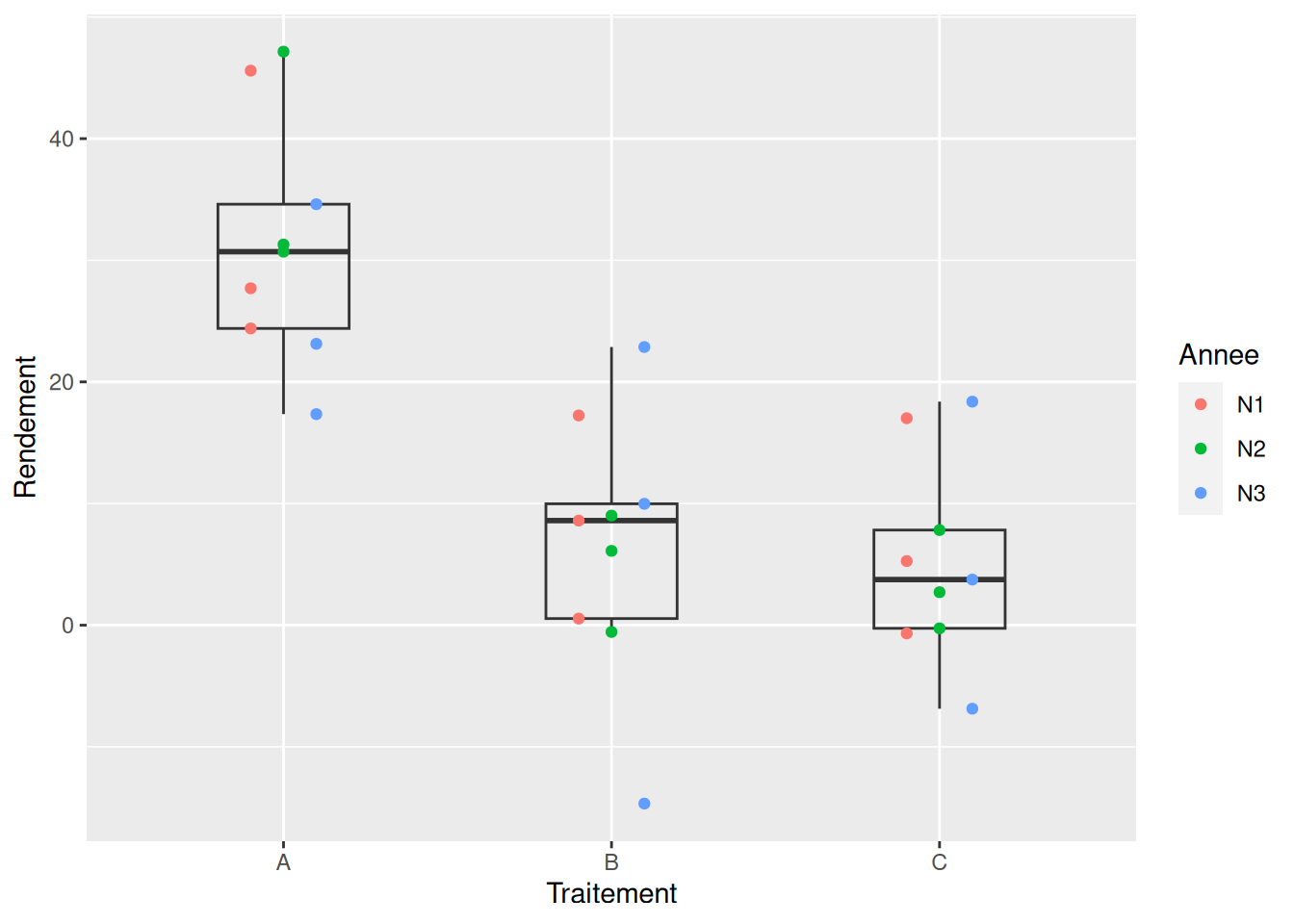
Le résultat du test ANOVA nous indique quels sont les facteurs qui expliquent le mieux la variance du rendement.
# écriture du modèle
modele <- lm(Rendement ~ Traitement * Annee, data = jeu)
# les hypothèses ont déjà été vérifiées dans le post ANOVA
# analyse de la variance
anova(modele)| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Traitement | 2 | 3885.35788 | 1942.67894 | 17.3081401 | 0.0000642 |
| Annee | 2 | 80.12607 | 40.06304 | 0.3569384 | 0.7046585 |
| Traitement:Annee | 4 | 166.07118 | 41.51780 | 0.3698994 | 0.8269386 |
| Residuals | 18 | 2020.33383 | 112.24077 | NA | NA |
Il n’y a que le traitement qui a un effet sur la variabilité du rendement et il n’y a pas d’interaction significative entre les années et le traitement.
2 Le package emmeans
Nous aimerions pouvoir comparer les traitements ente eux, parce que nous ne savons pas en quoi ils sont différents les uns des autres.
Par exemple, est-ce que la moyenne des rendements dans le traitement A est statistiquement supérieure à celles des deux autres traitements ?
Pour cela, nous allons procéder à des tests post-hoc, c’est-à-dire ayant lieu APRES la création du modèle.
C’est le job du package R emmeans !
emmeans signifie : estimated marginal means.
En l’occurence, la moyenne du rendement pour le traitement A, TOUTES CHOSES EGALES PAR AILLEURS (ici : pour une année donnée s’il y a un effet lié au facteur Annee), est une moyenne marginale à estimer.
Ce package est très polyvalent, très complet et surtout très pratique. Le package emmeans permet donc :
- d’estimer efficacement les moyennes marginales et leurs intervalles de confiance
- de tester si les moyennes sont statistiquement différentes deux à eux (par exemple).
ATTENTION ! N’utilisez SURTOUT PAS les intervalles de confiance des moyennes pour comparer vos traitements entre eux ! Une moyenne est un objet statistique en soi et une différence de moyennes en est un autre. Il ne faut pas mélanger ces concepts.
2.1 Visualisation des intervales de confiance des moyennes
emmip(modele, Annee ~ Traitement, CIs = TRUE)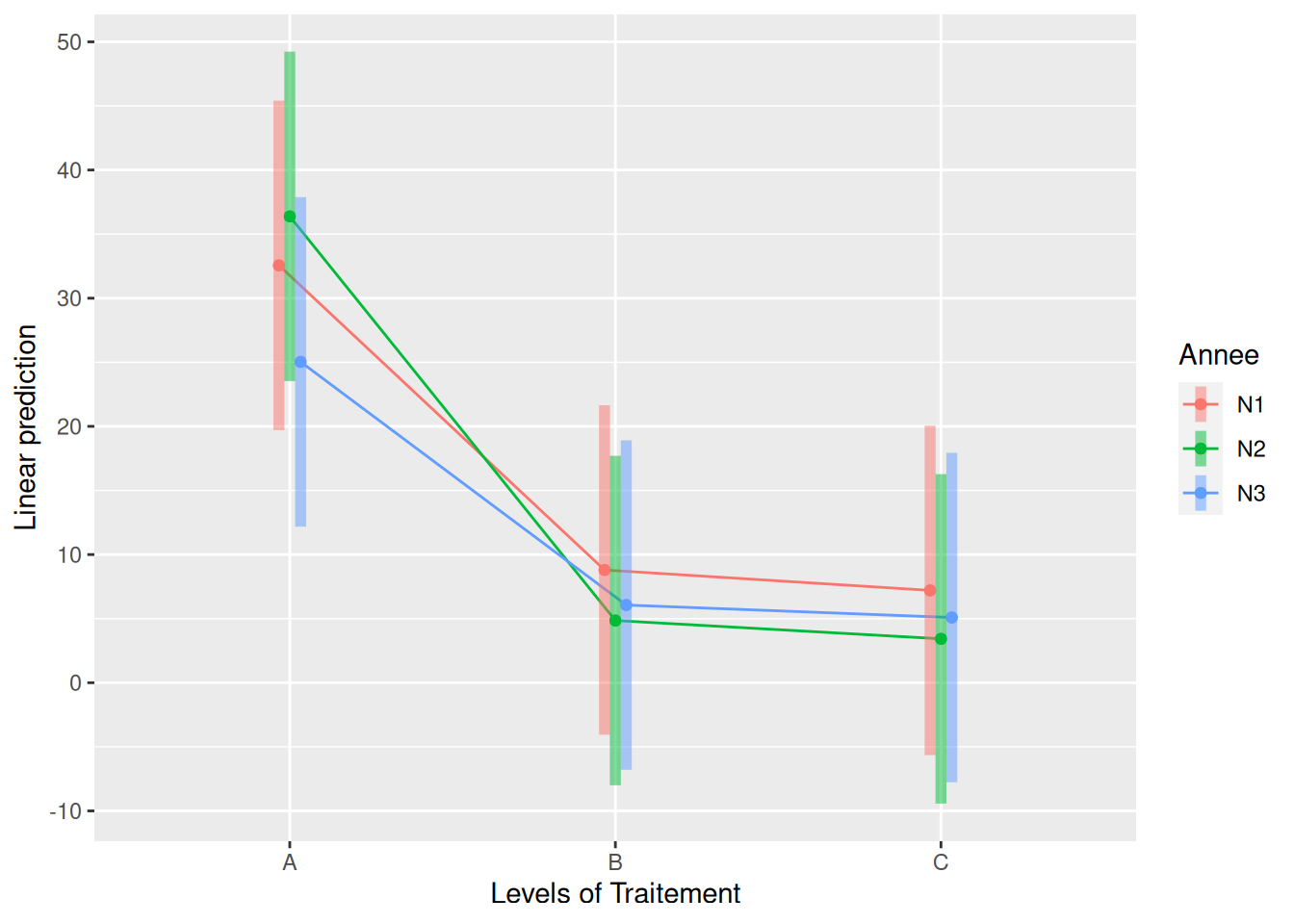
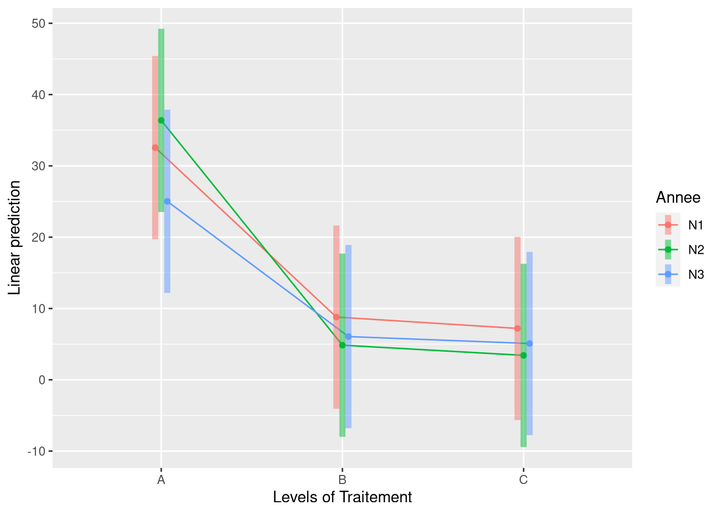
La fonction emmip() représente par défaut des intervales de confiance à 95%.
Si on répétait 100 fois l’expérience, les moyennes estimées tomberaient chacunes à peu près 95 fois dans les intervalles représentés.
2.2 Test de comparaison de moyennes
2.2.1 Sans interaction
Nous savons qu’il n’y a pas d’interaction significative entre Annee et Traitement grace au test ANOVA, nous pouvons nous permettre de comparer de manière globale A et B, A et C et B et C.
Comme l’effet Annee n’est pas significatif non plus, nous ne comparons pas les années entre elles.
Nous pouvons réécrire le modèle sans les facteurs et interactions qui ne sont pas significatifs :
modele_simple <- lm(Rendement ~ Traitement, data = jeu)Voici comment comparer les traitements deux à deux :
comparaison <- emmeans(modele_simple, ~ Traitement)
# test multiples de comparaison de moyennes deux à deux
pairs(comparaison)
## contrast estimate SE df t.ratio p.value
## A - B 24.76 4.58 24 5.404 <.0001
## A - C 26.09 4.58 24 5.694 <.0001
## B - C 1.33 4.58 24 0.291 0.9546
##
## P value adjustment: tukey method for comparing a family of 3 estimatesOn peut conclure ici que le traitement A est significativement différent des traitements B et C.
La notion de significativité est toute subjective, car elle dépend :
- de la valeur du seuil alpha du risque de première espèce (
0.05par défaut) et - de la configuration de l’ajustement (ajustement de Tukey par défaut).
Le risque de première espèce (la probabilité de dire “il y a une différence significative” à tort) augmente mathématiquement avec le nombre de tests effectués…
L’ajustement, c’est la correction appliquée aux p-valeurs des multiples tests effectuées pour comparer toutes les moyennes entre elles, afin de ne pas dépasser le fameux seuil alpha. Il existe un tas d’ajustements possibles, selon les cas de figure !
NB : Les moyennes marginales estimées (ainsi que leurs comparaisons) dépendent forcément d’un modèle. Exactement comme pour le résultat du test ANOVA, 2 modèles différents donneront des résultats différents. De même que pour un test ANOVA, il faut donc bien veiller à avoir un bon modèle, qui respecte les hypothèses de validation, avant de se lancer dans un test post-hoc.
2.2.2 Avec interaction
Il est judicieux d’étudier la différence entre les traitements année par année, dans le cas où il y a une interaction significative entre les années et les traitements.
Voici comment on pourrait le faire :
comparaison_inter <- emmeans(modele, ~ Traitement | Annee)
# test multiples de comparaison de moyennes deux à deux
pairs(comparaison_inter)
## Annee = N1:
## contrast estimate SE df t.ratio p.value
## A - B 23.766 8.65 18 2.747 0.0337
## A - C 25.358 8.65 18 2.931 0.0231
## B - C 1.592 8.65 18 0.184 0.9815
##
## Annee = N2:
## contrast estimate SE df t.ratio p.value
## A - B 31.531 8.65 18 3.645 0.0050
## A - C 32.959 8.65 18 3.810 0.0035
## B - C 1.428 8.65 18 0.165 0.9851
##
## Annee = N3:
## contrast estimate SE df t.ratio p.value
## A - B 18.970 8.65 18 2.193 0.0996
## A - C 19.943 8.65 18 2.305 0.0807
## B - C 0.974 8.65 18 0.113 0.9930
##
## P value adjustment: tukey method for comparing a family of 3 estimatesLorsqu’il y a beaucoup de tests, il est plus aisé de visualiser les résultats à l’aide d’un graphique :
# visualisation des résultats des tests
plot(comparaison_inter, comparisons = TRUE)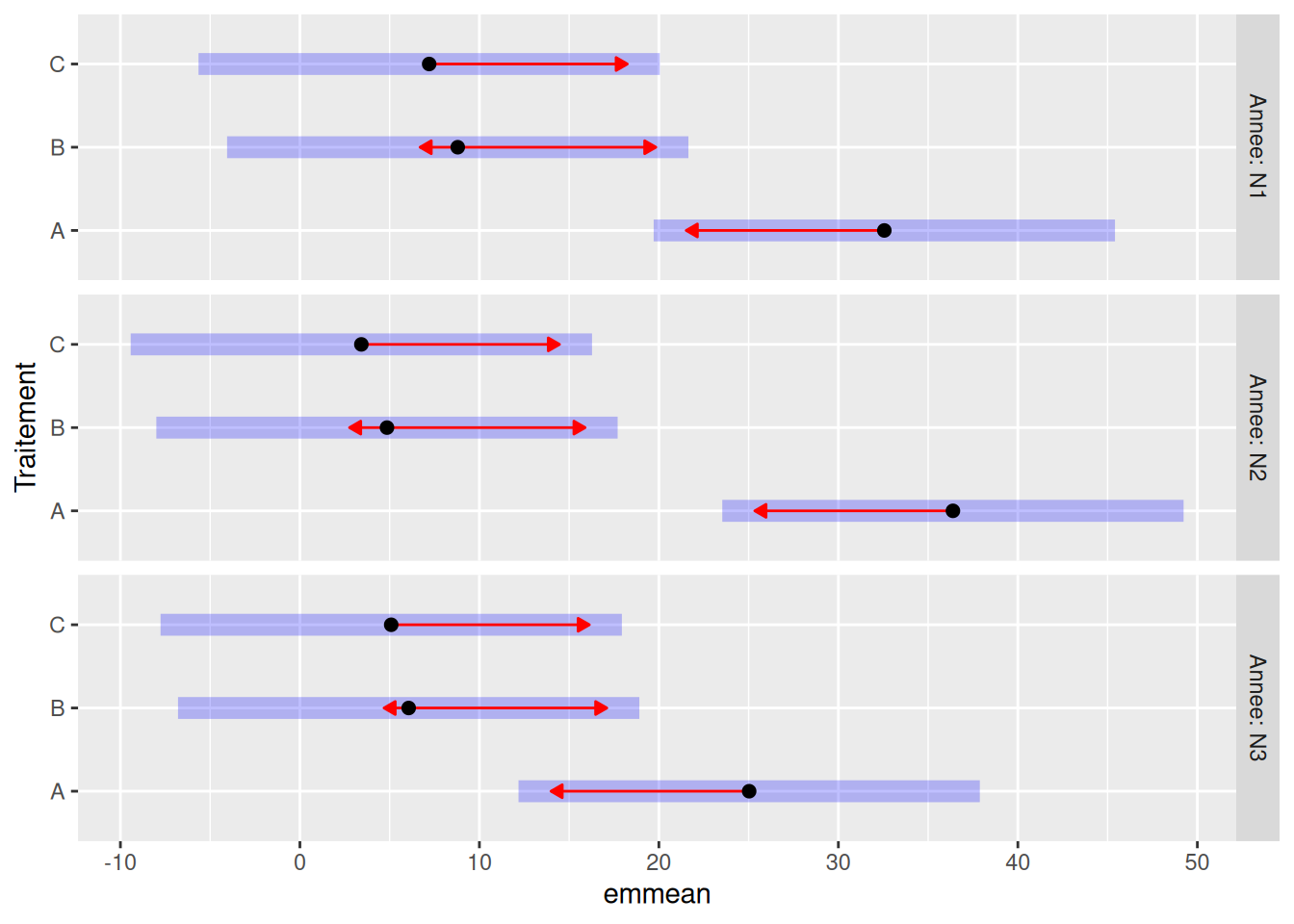
Dans ce dernier graphique, les barres bleues sont les intervales de confiance des moyennes estimées et les flèches rouges permettent de les comparer.
Il faut interpréter chaque sous-graphique indépendamment les uns des autres (chaque année ici). Si deux flèches se recoupent, alors la différence entre ces deux moyennes n’est pas significative.
Si l’interaction Annee:Traitement était significative, nous devrions conclure que pour l’année N3 il n’y a pas de différence entre les traitement, contrairement aux autres années.
Vous voyez que c’est un peu perturbant, nous avons utilisé les mêmes données, mais nous n’obtenons pas la même conclusion. Cela provient du fait que nous n’avons pas utilisé le même modèle ! Le modèle sans interaction force la différence entre traitements à rester la même pour toutes les années, alors que graphiquement on peut voir de légères variations.
Il peut aussi arriver le phénomène inverse, c’est-à-dire que l’ANOVA donne un effet significatif mais que emmeans ne trouve pas de différences significatives.
Honnêtement, à titre personnel, je n’aime pas trancher de manière aveugle quand une conclusion est ambivalente. Comme je l’ai dit plus haut, un seuil à 5% est subjectif. Mieux vaut afficher les p-valeurs du test ANOVA et des tests de comparaison multiples plutôt que de prendre une décision manichéenne.
Laissez vos lecteurs décider par eux-mêmes si vos découvertes sont significatives au regard des autres découvertes dans un contexte scientifique donné ;-)
3 Conclusion
Et finalement, me direz-vous, pourquoi ne pas calculer simplement la moyenne arithmétique ordinaire de tous les rendements du traitement A ?
Dans le cas, comme ici, où le plan factoriel est parfaitement équilibré (même nombre d’observations pour chaque modalité de chacun des facteurs) et qu’il n’y a pas d’interaction entre les facteurs, alors cela reviendra au même. Dans tous les autres cas, ce calcul simple peut mener à des interprétations totalement faussées, à cause des interactions et/ou d’un protocole déséquilibré.
Donc :
- faites des graphiques et
- utilisez le package emmeans pour calculer et comparer vos moyennes proprement.
Pour en savoir plus : https://cran.r-project.org/web/packages/emmeans/vignettes/basics.html
4 Remerciements
Une nouvelle fois, je tiens à remercier Claire Della Vedova et Nancy Rebout pour leurs précieux conseils !