Barres d'erreur

Dernière mise à jour le 2020-08-03 Tutoriel

Introduction

L’objectif de ce document est de vous montrer comment vous familiariser avec les barres d’erreur dans les graphiques en utilisant ggplot2. Il ne s’agirait pas d’entraîner une mauvaise interprétation de vos données suite à de malencontreux intervalles. Si vous confondez écart-type, erreur-type, écart inter-quartile, intervalle de confiance… L’enjeu est seulement de vous rafraîchir la mémoire et non de vous introduire ces notions en toute rigueur.

Attention ! Dans un souci de minimalisme éhonté, ceci n’est pas un tutoriel de R1, de dplyr2 ni encore de ggplot23,4. Pour en savoir plus sur ces sujets passionnants (oui, sincèrement), allez voir R for Data Science, disponible gratuitement en ligne5.
Certaines notions de statistiques descriptives sont présentées très succinctement ci-après et de manière beaucoup plus précise dans ce document un peu plus long, mais beaucoup plus rigolo : Statistiques pour statophobes6.

Confection des cookies du jeu de données

Voici comment simuler un jeu de données montrant l’évolution de la taille des cookies que je viens de faire. Il y en a(vait) n = 10. Leur diamètre a été mesuré avant (T0) et après (Tf) leur cuisson. Pour information, je les ai tous mangés, ils étaient très bons.

# manipulation de tableaux de données
library(dplyr) # group_by et summarise
# création de graphiques élégants
library(ggplot2) # ggplot
# personnaliser le thème des graphiques 
# attention il faut avoir la police xkcd pour que cela fonctionne correctement
library(xkcd) # theme_xkcd

n <- 10 # nombre de cookies

set.seed(3) # pour la reproductibilité du jeu de données
d0 <- rnorm(n, 40, 6) # diamètre initial

jeu <- data.frame(Cookie = factor(rep(1:n, 2)), 
  Temps = rep(c("T0", "Tf"), each = n), 
  Diametre = round(c(d0, d0 + rnorm(n, 20, 10)))
  )

jeu
Cookie Temps Diametre
1 T0 34
2 T0 38
3 T0 42
4 T0 33
5 T0 41
6 T0 40
7 T0 41
8 T0 47
9 T0 33
10 T0 48
1 Tf 47
2 Tf 47
3 Tf 54
4 Tf 56
5 Tf 63
6 Tf 57
7 Tf 51
8 Tf 60
9 Tf 65
10 Tf 70

Nous souhaitons (ardemment) comparer le diamètre des cookies entre le moment où ils ont été déposé sur la plaque et leur sortie du four. En effet, j’ai remarqué qu’ils avaient tendance à s’aplatir pendant la cuisson.

Nous pouvons résumer les données ainsi :

jeu %>% 
  group_by(Temps) %>% 
  summarise(Diam_Moyen = mean(Diametre), 
    Diam_EcartType = sd(Diametre)
    )
Temps Diam_Moyen Diam_EcartType
T0 39.7 5.334375
Tf 57.0 7.630349

Mais je trouve qu’un tableau est souvent moins parlant qu’un graphique, alors… Allons-y !

Observation des données

Ici, je pose la base des graphiques qui suivront. Cela évitera ainsi les redondances de code. Les deux premières lignes (ggplot et aes) sont essentielles, le reste est totalement optionnel.

base <- ggplot(jeu) +
  # définir le rôle des variables
  aes(x = Temps, y = Diametre, colour = Temps, fill = Temps) + 
  # modifier les titres des axes
  labs(x = ""
       , y = ""
       , subtitle = "Diametre - mm") + 
  # l'axe y commence par 0 pour une représentation plus réaliste
  coord_cartesian(ylim = c(0, max(jeu$Diametre) + 5), default = T) + 
  # modifie les couleurs manuellement pour colour et fill en même temps
  scale_colour_manual(aesthetics = c("colour", "fill") 
                      , values = c(T0 = "#e69f02", Tf = "#a65c34")
                      ) +
  theme_xkcd() + # mon thème préféré
  theme(legend.position = "none" # légende ici inutile
        # rajout des lignes représentant les axes
        , axis.line = element_line(colour = "black"
                                   , arrow = arrow(length = unit(2, "mm"))
                                   )
        , plot.background = element_rect(fill = "transparent", colour = NA)
        , panel.background = element_rect(fill = "transparent", colour = NA)
        )

Tout d’abord, observons nos données brutes :

base + 
  geom_point(size = 2)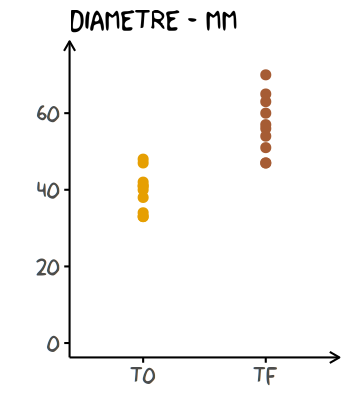

Attention ! Les données sont appariées, c’est-à-dire que les cookies mesurés sont les mêmes entre T0 et Tf. Autrement dit, les deux lignes suivantes correspondant aux mesures effectuées sur le premier cookie ne sont pas indépendantes.

jeu %>% filter(Cookie == 1)
Cookie Temps Diametre
1 T0 34
1 Tf 47

Par la suite, nous ne prendrons pas cela en compte. Pour comparer les moyennes à T0 et Tf en toute rigueur , il faudrait faire un test apparié et/ou un modèle linéaire mixte en mettant Cookie en variable aléatoire. Mais ce n’est pas le sujet ici…

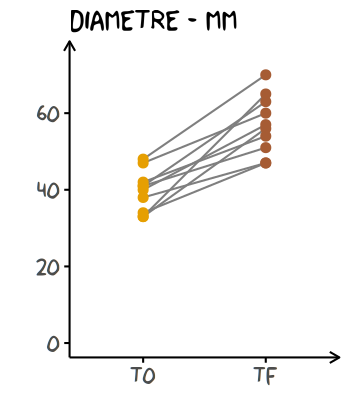
Voilà un exemple de représentation de la non-indépendance de ces données :

base +
  # nouveau rôle (aes) défini afin de tracer une ligne par Cookie (group)
  geom_line(aes(group = Cookie) 
            , colour = "grey50" # couleur (unique) des lignes
            ) +
  # ordre des commandes important
  # pour que les points viennent par-dessus les lignes
  geom_point(size = 2)

Description des données

Pour observer la distribution des données, il est possible de construire un histogramme ou de tracer les densités :

base +
  # création de nouveaux rôles (aes)
  geom_freqpoly(aes(x = Diametre, colour = Temps)
                # les rôles définis dans base ne sont pas pris en compte
                , inherit.aes = F
                # largeur des classes
                , binwidth = 4
                # épaisseur du trait
                , size = 1
                ) +
  # retrouve le système de coordonnées par défaut
  coord_cartesian()
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.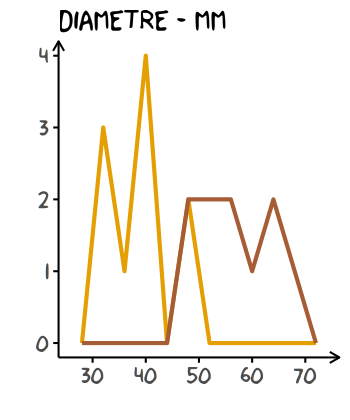

base +
  geom_density(aes(x = Diametre, colour = Temps) 
               , inherit.aes = F 
               , size = 1
               , adjust = 1.5 # paramètre de lissage
               ) +
  coord_cartesian()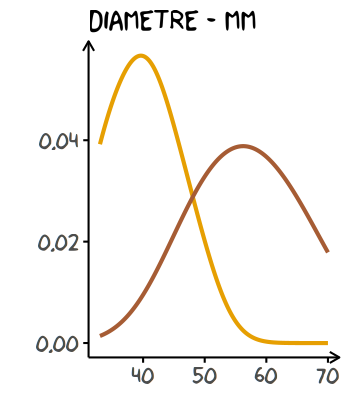

Plus souvent, on a envie de faire un diagramme en boîtes (boxplot) ou encore un diagramme en bâtons (barplot) :

base +
  geom_boxplot(width = 0.3 # largeur des boîtes
               , size = 1
               , colour = "grey20" # couleur (unique) des contours
               ) +
  # ajout des tailles d'échantillonage
  annotate("text", x = 1:2, y = 75, label = paste("n =", n), family = "xkcd")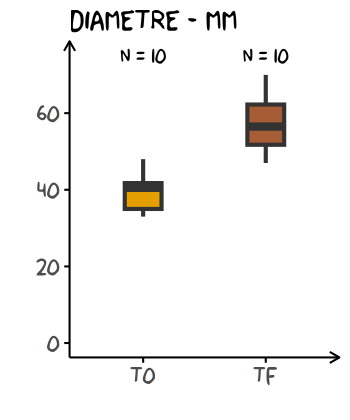

base +
  # ajout des bâtons
  geom_bar(stat = "summary" # personnalise la hauteur des bâtons
           , fun = "mean" # hauteur des bâtons = moyenne des observations
           , width = 0.3 # largeur des bâtons
           , colour = "grey20" # couleur des bâtons
           , size = 1 # largeur du trait
           ) +
  # ajout des barres d'erreur
  geom_linerange(stat = "summary" # personnalise le calcul des barres d'erreur
                 # fonction qui renvoie la moyenne 
                 # et l'intervalle de confiance de la moyenne 
                 # à 95% selon une distribution de Student 
                 # à n-1 degrés de liberté
                 , fun.data = ~ mean_se(.x, mult = qt(0.975, length(.x) - 1))
                 , colour = "grey20"
                 , size = 1 
                 ) +
  # ajout des tailles d'échantillonage
  annotate("text", x = 1:2, y = 75, label = paste("n =", n), family = "xkcd")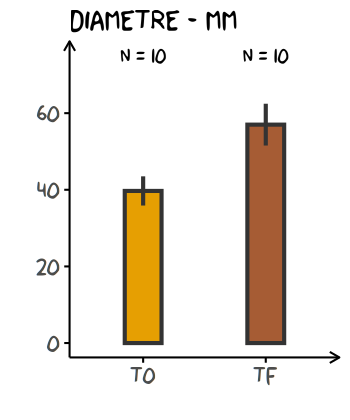

Remarque : Le calcul des intervalles de confiance des moyennes correspond à \[ IC(95\%) = \mu \pm dispersion \times quantile(95\%)\] avec \(\mu\) la moyenne des observations.

L’indicateur de dispersion est l’erreur-type \(se = \frac{sd}{\sqrt(n)}\) (nous nous intéressons à la dispersion de la moyenne), avec \(sd\) l’écart-type et \(n\) le nombre d’observations.
Les mesures sont continues, supposées normalement distribuées et \(n < 30\), donc le choix de la distribution des données se porte sur une loi de Student à \(n-1 = 9\) degrés de liberté.

Ainsi, en notant \(qt\) le quantile de Student, on a : \[ IC(95\%) = \mu \pm \frac{sd}{\sqrt(n)} \times qt(95\%, n-1)\] N’oubliez pas d’adapter le choix de votre quantile aux hypothèses que valident (ou pas) vos données !

Mais ces quatre derniers graphiques restent moins informatifs qu’un graphique qui conserve encore les observations les plus brutes possibles – surtout lorsque n est faible. En effet, les trois premiers contiennent des calculs réduisant l’information des données brutes. De plus, les densités et les diagrammes en boîtes et en bâtons ne montrent pas par défaut la taille du groupe d’échantillonnage, qu’il est (malheureusement) courant d’omettre. Par ailleurs, la distribution sous-jacente des données est cachée dans les diagrammes en boîtes et en bâtons. Comme l’histogramme n’est pas la représentation la plus aisée à lire au premier regard, vous pouvez utiliser geom_jitter() pour un petit nombre de points et geom_violin() pour un plus grand nombre de points.

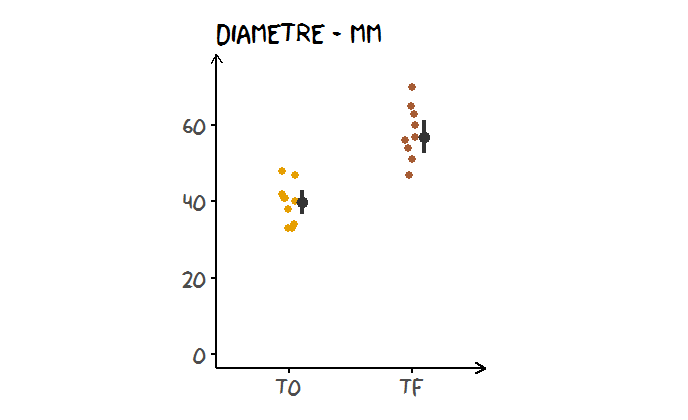
Ci-dessous une proposition d’ajout des barres d’erreur dans un graphique conservant l’information des données brutes :

base +
  geom_jitter(size = 1.5, width = 0.07, height = 0) +
  # ajout des barres d'erreur, 
  # pointrange rajoute un point pour indiquer la position de la moyenne
  geom_pointrange(stat = "summary" 
                  , fun.data = ~ mean_se(.x, mult = qt(0.975, length(.x) - 1))
                  # décale les barres des observations
                  # pour éviter le chevauchement
                  , position = position_nudge(x = 0.1)
                  , colour = "grey20"
                  , size = 1
                  , fatten = 2 # règle la taille du point central
                  )

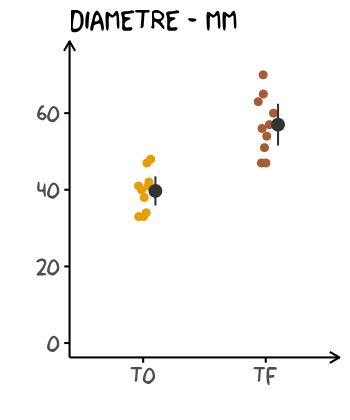
C’est donc ce que je vous recommande de faire à chaque fois que vous désirerez manger des cookies !

Comme le jeu de données est simulé (vos données dans vos rêves !), les intervalles de confiance ne se recoupent pas. C’est un premier indicateur sympathique pour avancer que les moyennes sont statistiquement différentes avec un seuil de 5%.

Cela ne vous empêchera pas, bien entendu, de faire un modèle inférentiel pour vérifier plus rigoureusement ! Je rappelle à tout bon entendeur que nous avons formulé implicitement une hypothèse forte d’indépendance des données : pour prouver que les deux moyennes sont bien différentes, il faudrait vérifier s’il y a un effet Cookie.

Il existe tout de même un moyen de faire des barres d’erreur sans hypothèse de départ sur la distribution des observations, c’est le bootstrap. Sans rentrer dans les détails7, c’est une méthode de rééchantillonnage non paramétrique donc moins puissante (il faudra davantage d’obervations pour détecter une différence qu’avec une méthode paramétrique). En terme de code, avec ggplot2, il suffit de changer la fonction de calcul des erreurs :

base +
  geom_jitter(size = 1.5, width = 0.07, height = 0) +
  # ajout des barres d'erreur, 
  # pointrange rajoute un point pour indiquer la position de la moyenne
  geom_pointrange(stat = "summary" 
                  , fun.data = mean_cl_boot
                  # décale les barres des observations
                  # pour éviter le chevauchement
                  , position = position_nudge(x = 0.1)
                  , colour = "grey20"
                  , size = 1
                  , fatten = 2 # règle la taille du point central
                  )

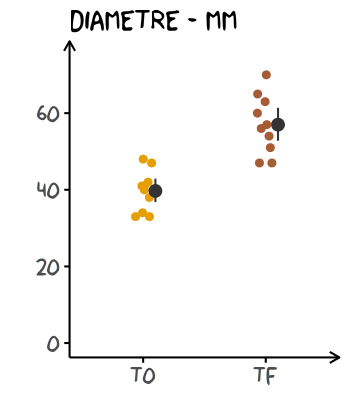
Remerciements

Spéciale dédicace à Christel Michel qui m’a fait prendre conscience à quel point il était urgent que je créée ce document. Merci Christel 😉 !
Je remercie Tom Doizy pour l’illustration 3D de cookies trop la classe.
Merci à mes fidèles relecteurs : Marion Ramos, Ismaël Houillon et Paola Campos.

Bibliographie

1.
R Core Team. R: A language and environment for statistical computing. (R Foundation for Statistical Computing, 2020).
2.
Wickham, H., François, R., Henry, L. & Müller, K. Dplyr: A grammar of data manipulation. (2020).
3.
Wickham, H. ggplot2: Elegant graphics for data analysis. (Springer-Verlag New York, 2016).
4.
Wickham, H. et al. ggplot2: Create elegant data visualisations using the grammar of graphics. (2020).
5.
Wickham, H. & Grolemund, G. R for data science: Import, tidy, transform, visualize, and model data. (" O’Reilly Media, Inc.", 2016).
6.
Poinsot, D. Statistiques pour statophobes. (2004).
7.
Efron, B. Bootstrap methods: Another look at the jackknife. The Annals of Statistics 7, 1–26 (1979).
Comprendre Transmettre
Anna Doizy
Anna Doizy
Chercheuse, consultante et formatrice freelance
Libre comme l’R

Méthodologie scientifique et analyses de données statistiques