Quand utiliser l'ANOVA ?
L’ANOVA est un type de modèle paramétrique où la variable à expliquer (la réponse) est numérique et les variables explicatives sont catégorielles (des facteurs pour R). Un modèle linéaire, un modèle linéaire généralisé, ou même un modèle mixte par exemple peuvent être des ANOVA (au sens large : voici une définition plus poussée) tant qu’il n’y a pas de variable numérique dans les variables explicatives.
1 Création du jeu de données illustratif
Par exemple, on veut étudier le rendement de canne à sucre entre différentes années (considérées comme indépendantes ici) pour certains traitements selon un plan factoriel complet. Il y a 3 parcelles (répétition) pour chaque combinaison de traitement/année. Le rendement est la variable à expliquer et les années et traitements sont les deux facteurs (potentiellement) explicatifs.
# chargement des packages
library(tidyverse)
library(skimr)
# création d'un jeu de données illustratif
set.seed(123) # pour fixer l'aléatoire et retrouver le même jeu de données
jeu <- tibble(
Traitement = rep(LETTERS[1:3], each = 9) %>% factor(),
Annee = paste0("N", rep(1:3, times = 3, each = 3)) %>% factor(),
Rendement = c(rnorm(9, mean = 60, sd = 10), rnorm(9, mean = 35, sd = 10), rnorm(9, mean = 40, sd = 10))
)
skim(jeu) # équivalent plus évolué de summary() ;-)| Name | jeu |
| Number of rows | 27 |
| Number of columns | 3 |
| _______________________ | |
| Column type frequency: | |
| factor | 2 |
| numeric | 1 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| Traitement | 0 | 1 | FALSE | 3 | A: 9, B: 9, C: 9 |
| Annee | 0 | 1 | FALSE | 3 | N1: 9, N2: 9, N3: 9 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| Rendement | 0 | 1 | 44.38 | 15.38 | 15.33 | 33.23 | 39.98 | 53.76 | 77.15 | ▁▇▂▅▁ |
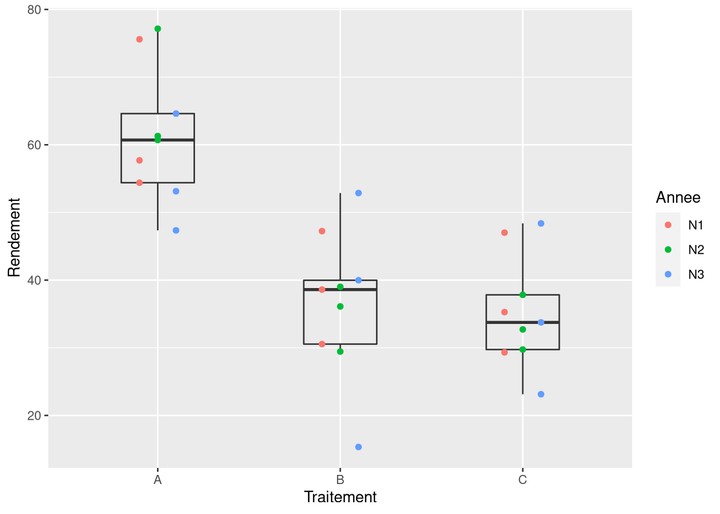
2 Visualisation du plan d’expérience
# visualisation du plan d'expérience
jeu %>%
count(Traitement, Annee) %>%
ggplot() +
aes(x = Traitement, y = Annee, size = n) +
geom_point()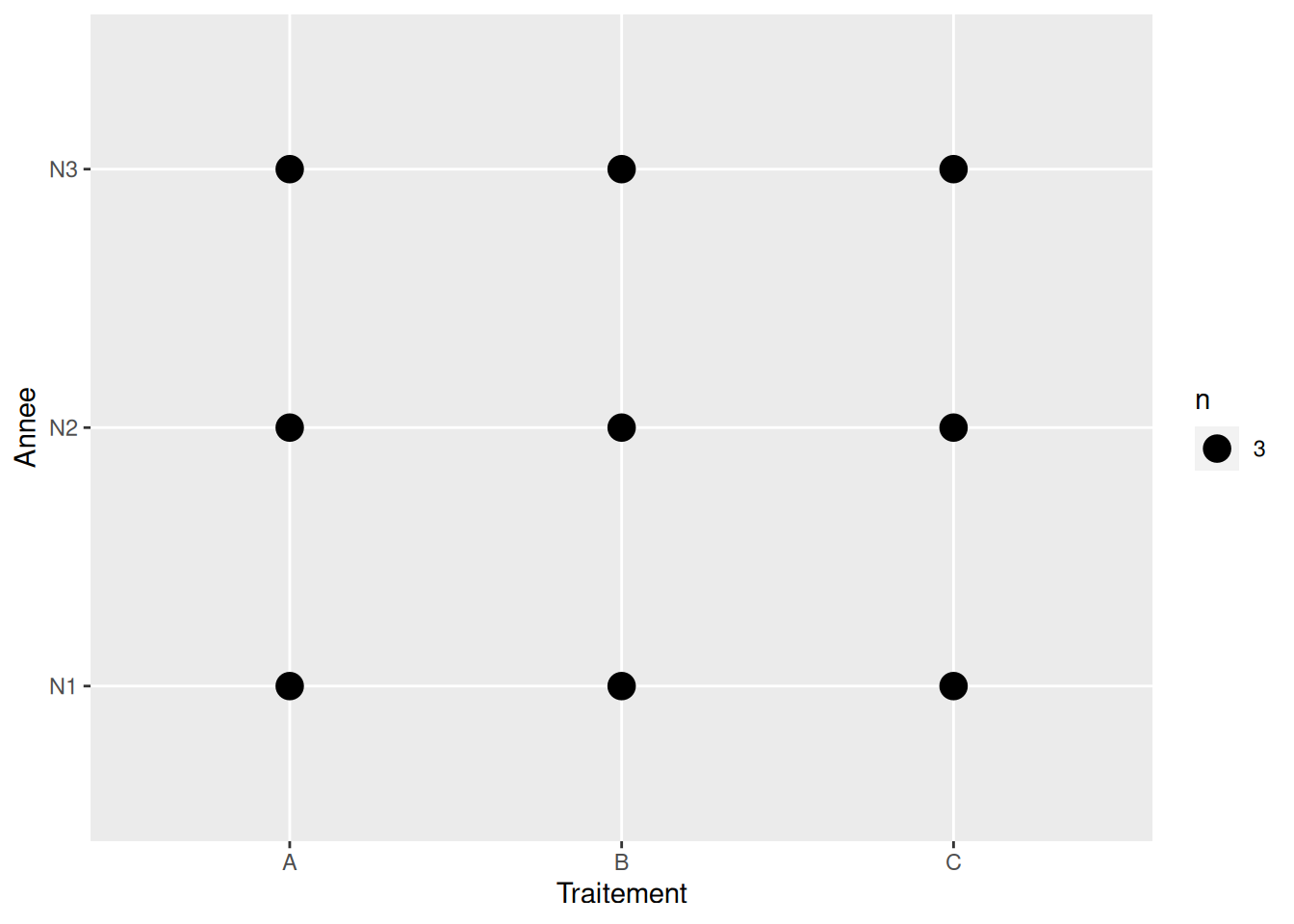
# on peut le faire avec la fonction ftable() aussi3 L’ANOVA en soi
On utilise le test ANOVA (analysis of variance) pour comprendre la part de variabilité des observations (la variable réponse) imputable à chacun des facteurs (ainsi que de leurs interactions, si elles sont prises en compte dans le modèle). C’est-à-dire, quelle variabilité du rendement est expliquée par le côté temporel (les années) et les différents traitements ? Peut-être que les traitements n’ont aucun effet sur la variabilité du rendement ?
Petite parenthèse :
Je distingue, de manière tout à fait personnelle, les notions de modèle ANOVA (le processus qui permet d’estimer des paramètres à partir de nos données) et de test ANOVA (on fait des tests statisiques). Je trouve que c’est trompeur, on utilise le même mot pour plusieurs choses différentes. Alors, j’ai choisi de créer mes mots ;)
Il est fondamental de procéder par étapes et de ne pas foncer tête baissée dans le test ANOVA, sous peine de choses affreuses. Par exemple, conclure à tort qu’il y a un effet significatif.
3.1 Regarder les données brutes
D’abord, on regarde les données brutes avec un scatter plot (et pas des box plot seuls, s’il vous plaît ! Allez voir pourquoi ici).
# visualisation des données
ggplot(jeu) +
aes(x = Traitement, y = Rendement) +
geom_boxplot(fill = "transparent", width = 0.4, outlier.shape = NA) +
geom_point(aes(color = Annee), position = position_dodge(width = 0.3))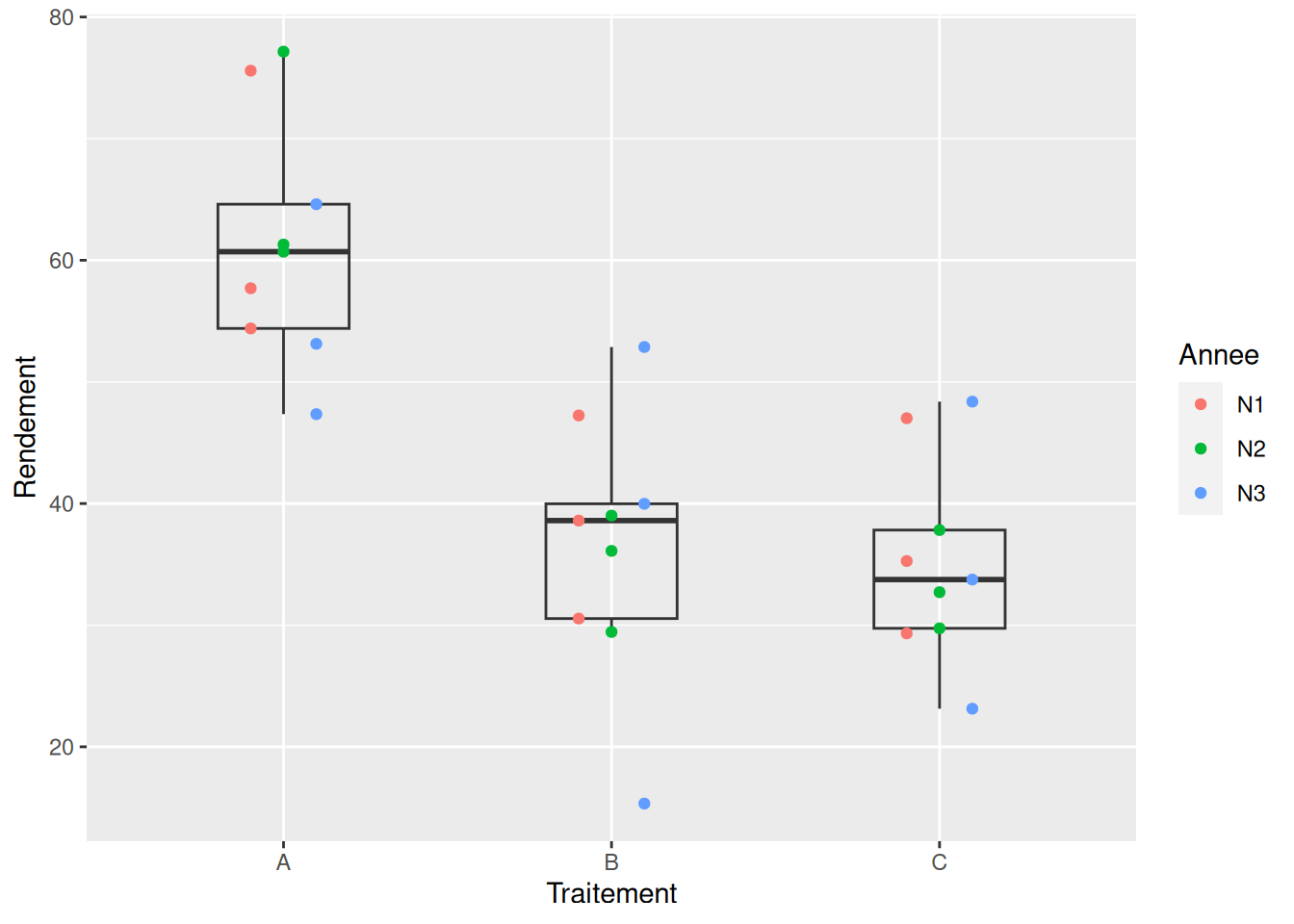
3.2 Ecrire le modèle
Ensuite, on écrit le modèle. Ici, je choisis d’écrire le modèle complet, comprenant l’interaction entre les deux facteurs.
(Notez que ~ A * B, peut également s’écrire ~ A + B + A:B)
On peut dire que ceci est un modèle “de type ANOVA”, car les variables explicatives sont qualitatives.
# écriture du modèle
modele <- lm(Rendement ~ Traitement * Annee, data = jeu)3.3 Vérifier les hypothèses du modèle
On vérifie les hypothèses sous-jacentes du modèle. Dans le cas d’un modèle linéaire :
- indépendance des observations,
- homogénéité de la variance et normalité des résidus du modèle,
- présence d’observations d’influence,
- sens biologique/physique - si le modèle prédit un rendement négatif , c’est pas ouf.
# vérification visuelle des hypothèses du modèle
plot(modele)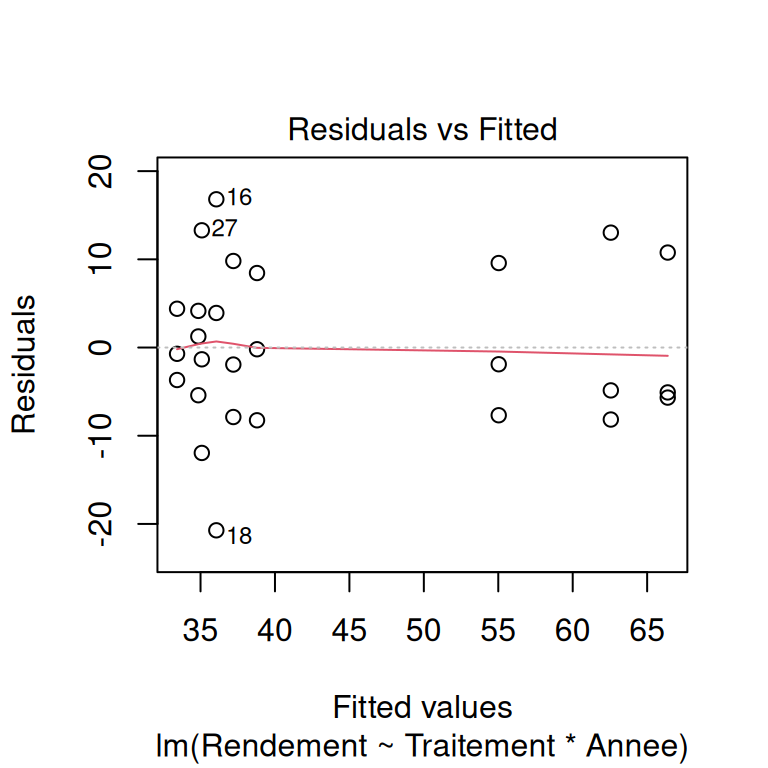
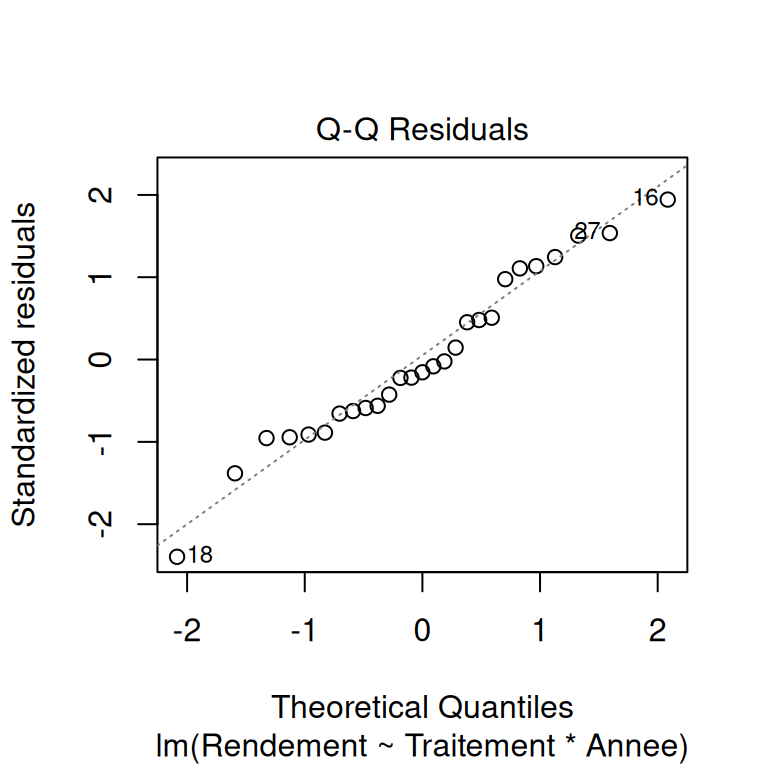
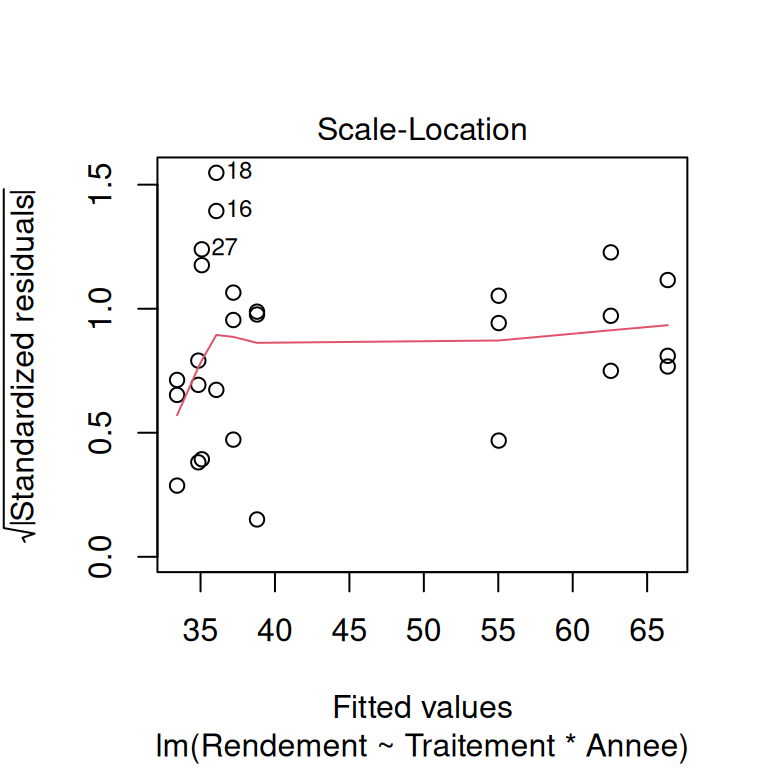
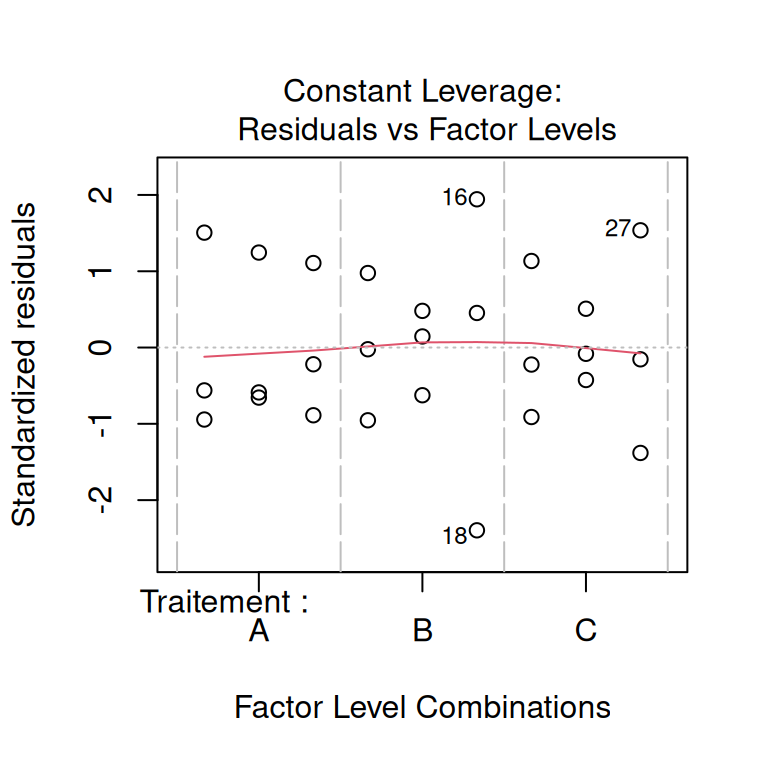
Pour apprendre à lire ces graphiques de validation, vous pouvez commencer par ici.
3.4 Procéder à l’analyse de la variance : le test ANOVA
SI les conditions d’application sont respectées, ALORS, on peut enfin analyser les résultats du modèle :
# analyse de la variance
anova(modele)| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Traitement | 2 | 3885.35788 | 1942.67894 | 17.3081401 | 0.0000642 |
| Annee | 2 | 80.12607 | 40.06304 | 0.3569384 | 0.7046585 |
| Traitement:Annee | 4 | 166.07118 | 41.51780 | 0.3698994 | 0.8269386 |
| Residuals | 18 | 2020.33383 | 112.24077 | NA | NA |
La colonne Pr(>F) donne, pour chaque facteur, la p-valeur de la statistique de test F, c’est-à-dire la probabilité que la F-value soit bien celle calculée en supposant que l’hypothèse nulle (il n’y a pas de différence entre les moyennes des groupes) est vraie.
On en conclue, sans surprise (regardez le code pour créer le jeu de données), que la variabilité du rendement est expliquée par la variable traitement et qu’il n’y a pas d’interaction ni d’effet lié à l’année.
4 Pour aller plus loin
Malheureusement (pour vous), il existe différents types de tests ANOVA (I, II et III), parce que la variance peut se découper de différentes manières :
- Quelle est la différence entre ces tests ?
- Dans le doute, utilisez le type III. Comment faire ?
Pour mieux comprendre les sombres histoires de p-valeurs, vous pouvez lire mon article dédié :
Allez, bon courage !
5 Remerciements
Voici une section dédiée à mes deux relectrices biostatisticiennes. Je les remercie très fort pour leurs propositions d’amélioration de ce texte. J’ai tout fait pour prendre en compte leurs remarques !